三道算法题实现

发表于 分类于
本文字数： 3.2k 阅读时长 ≈ 5 分钟

  三道算法的实现，分别是字符串内所有数字之和、多项式简单卷积实现、怪物牛的生长数量。

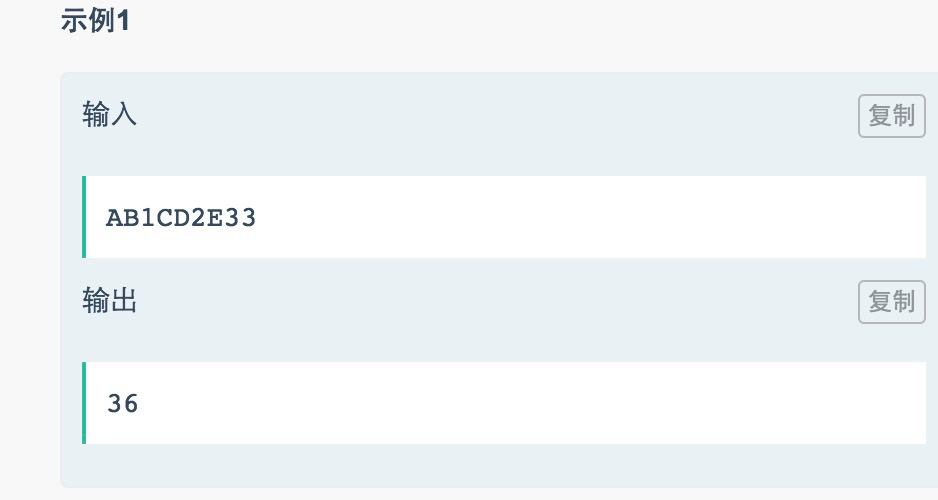
1、字符串内数字之和



这个没什么好说的，实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
#include<string>
using namespace std;
int ssum(string &str)
{
    int ans = 0;
    int pos = 1;
    int num = 0;
    for (size_t i = 0; i < str.length(); i++)
    {
        
        if(str[i]>='0'&&str[i]<='9'){
            num = 10 * num + (str[i] - '0') * pos;
        }
        else{
                ans += num;
                num = 0;
                if(str[i]=='-'){
                    pos = pos == 1 ? -1 : 1;
                }
                else{
                    pos = 1;
                }
            }
    }
    ans += num;
    return ans;
}
int main()
{
    string s1 = "ab-1.3d----5ef--122";
    cout << ssum(s1);
}

好像也有一些需要说明的，首先使用string类型，然后对比字符以及加减获得数值，常规操作。唯一需要注意的就是这个-1的pos值，有个设定，就是每次遇到-的时候需要反变换，这里用了pos = pos == 1 ? -1 : 1;来完成，直接乘-1也是可以的。但是注意pos结束一个流程后要归位1。和上面得到连续的数的操作一样。

2、多项式简单卷积



这道题我偷懒了，直接用数组做了，而且直接将大小都设置为4阶了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
using namespace std;
int main()
{
    int a[10];
    int s1[2];
    int s2[2];
    for (int i = 0; i < 10; i++)
    {
        cin >> a[i];
    }
    int b[10];
    for (int j = 0; j < 10;j++){
        cin >> b[j];
    }
    for (int k = 8; k > -1;k--){
        int ansr = 0;
        int ansi = 0;
        for (int q = 0; q <= k;q++){
            if (2 * q + 1 < 10 && 2 * (k - q) + 1 < 10)
            {
                s1[0] = a[2 * q];
                s1[1] = a[2 * q + 1];
                s2[0] = a[2 * (k - q)];
                s2[1] = a[2 * (k - q) + 1]; 
                int tempr = s1[0] * s2[0] - s1[1] * s2[1];
                int tempi = s1[1] * s2[0] + s1[0] * s2[1];
                ansr += tempr;
                ansi += tempi;   
            }
        }      
        cout << ansr << endl;
        cout << ansi << endl;
    }
    return 0;
}

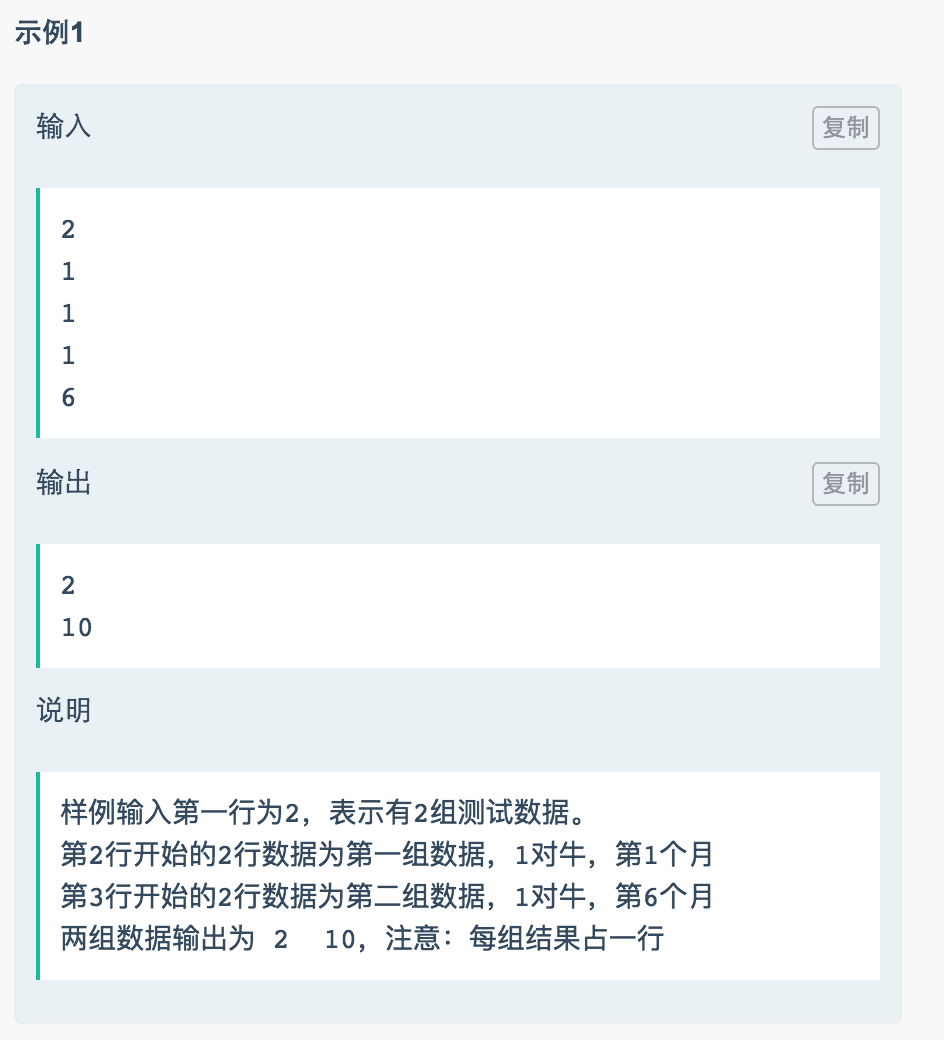
3、怪物牛的生长数量




这道题猛一看无从下手，但是直觉肯定告诉你用递归来做应该不会错，而且用递归很可能会导致时间复杂度达到O(2n)，但这都是后话了，先把逻辑理顺，说不定递归就能改成迭代形式了。
为此，我们需要仔细分析题目，一对牛生一对牛，可以理解为1生1，同时你发现，1对牛和m对牛之间是互不干扰的，也就是m只是一个乘积数，你分析1对牛的结果乘m就是m对牛的结果。做题最重要的就是动笔（捂脸笑），分析如下：

不知道你是否能看出4月到5月、5月到6月、6月到7月的变化。是不是下一个月的数量为上个月的数量加上了4个月前的数量，满足了f(n)=f(n-1)+f(n-4)。可以理解为一对牛从出生到产子需要4个月，所以4个月后数量就不是单纯的+1，而是+f(n-4)。而很明显这个递归式时间复杂度指数级，而且可以用迭代替换实现，交给大家了，我就写一个递归实现的就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
using namespace std;

int funnum(int m, int n){
    if(n==0){
        return m;
    }
    else if(n==1){
        return 2 * m;
    }2
    else if(n==2){
        return 3 * m;
    }
    else if(n==3){
        return 4 * m;
    }
    return funnum(m, n - 1) + funnum(m, n - 4);
}
int main(){
    int a = 0;
    cin >> a;
    int b[2*a];
    for (int j = 0; j < 2 * a;j++){
        cin >> b[j];
    }
    for (int i = 0; i < 2 * a; i = i + 2)
        {
            int c = funnum(b[i], b[i + 1]);
            cout << c << endl;
        }
        return 0;
}

代码都挺朴实无华的，不要乱搞骚操作，一是某些写法对运行时间的提升不大，二是记性不好写错了改bug也费时间。